

IQ SCORES
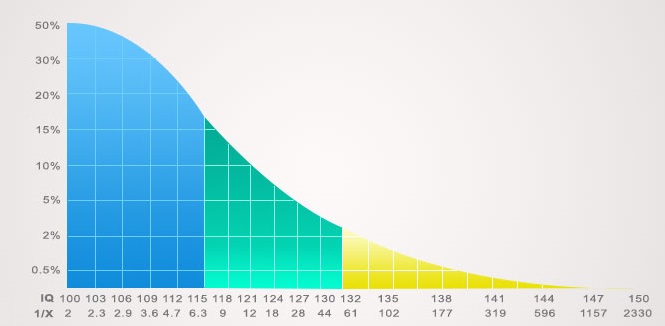
Distribution curve IQ test population ratio ( from the IQ 100-150 )
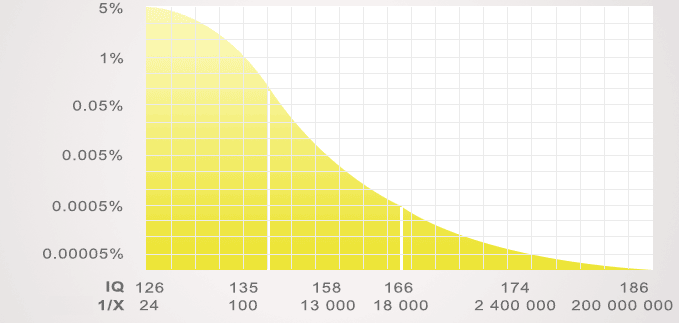
Distribution curve IQ test population ratio ( from the IQ 126-186 )
IQ Scores:
IQ Test from 85 belongs to the low (16% rate)
IQ Test from 85-115, classified as normal (68% rate)
IQ Test from 115-130, kind of intelligence (14% rate))
IQ Test from 130-145, being very intelligent (rate 2%)
IQ Test from 145 onwards, genius or mostly genius (ratio 0.1% )
Copyright © International High IQ Society. All rights reserved
